7. Basic cube mathematics

The section Navigating a cube highlighted that every cube has a data attribute; this attribute can then be manipulated directly:

cube.data -= 273.15

The problem with manipulating the data directly is that other metadata may become inconsistent; in this case the units of the cube are no longer what was intended. This example could be rectified by changing the units attribute:

cube.units = 'celsius'

Note

iris.cube.Cube.convert_units() can be used to automatically convert a cube’s data and update its units attribute. So, the two steps above can be achieved by:

cube.convert_units('celsius')

In order to reduce the amount of metadata which becomes inconsistent, fundamental arithmetic operations such as addition, subtraction, division and multiplication can be applied directly to any cube.

7.1. Calculating the difference between two cubes

Let’s load some air temperature which runs from 1860 to 2100:

filename = iris.sample_data_path('E1_north_america.nc')
air_temp = iris.load_cube(filename, 'air_temperature')

We can now get the first and last time slices using indexing (see Reducing a Cube for a reminder):

t_first = air_temp[0, :, :]
t_last = air_temp[-1, :, :]

And finally we can subtract the two. The result is a cube of the same size as the original two time slices, but with the data representing their difference:

>>> print t_last - t_first
unknown / (K)                       (latitude: 37; longitude: 49)
     Dimension coordinates:
          latitude                           x              -
          longitude                          -              x
     Scalar coordinates:
          forecast_reference_time: 1859-09-01 06:00:00
          height: 1.5 m
     Attributes:
          history: air_temperature - air_temperature (ignoring forecast_period, time)

Note

Notice that the coordinates “time” and “forecast_period” have been removed from the resultant cube; this is because these coordinates differed between the two input cubes. For more control on whether or not coordinates should be automatically ignored iris.analysis.maths.subtract() can be used instead.

7.2. Combining multiple phenomena to form a new one

Combining cubes of potential-temperature and pressure we can calculate the associated temperature using the equation:

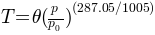
Where 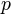is pressure, 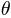is potential temperature, 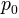is the potential temperature reference pressure and 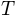is temperature.

First, let’s load pressure and potential temperature cubes:

filename = iris.sample_data_path('colpex.pp')
phenomenon_names = ['air_potential_temperature', 'air_pressure']
pot_temperature, pressure = iris.load_cubes(filename, phenomenon_names)

In order to calculate 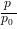we can define a coordinate which represents the standard reference pressure of 1000 hPa:

import iris.coords
p0 = iris.coords.AuxCoord(1000.0,
                          long_name='reference_pressure',
                          units='hPa')

We must ensure that the units of pressure and p0 are the same, so convert the newly created coordinate using the iris.coords.Coord.convert_units() method:

p0.convert_units(pressure.units)

Now we can combine all of this information to calculate the air temperature using the equation above:

temperature = pot_temperature * ( (pressure / p0) ** (287.05 / 1005) )

Finally, the cube we have created needs to be given a suitable name:

temperature.rename('air_temperature')

The result could now be plotted using the guidance provided in the Plotting a cube section.

A very similar example to this can be found in Deriving Exner Pressure and Air Temperature.